Malen nach Zahlen
Die Bildverarbeitung in Digitalkameras und in Anwendungen wie Photoshop folgt mathematischen Formeln, während es uns ja eigentlich um Bilder geht. Wie bringt man Rechenregeln und unsere visuelle Wahrnehmung zusammen?
In der Fotografie ebenso wie in der Bildbearbeitung geht es naturgemäß um Bilder. Jedenfalls für uns als Fotografen und Bildbearbeiter. Wenn wir auf den Auslöser drücken, haben wir eine Vorstellung davon, was für ein Bild wir aufnehmen wollen, und auch das erhoffte Ergebnis einer Bearbeitung in Photoshop stellen wir uns visuell vor.
Doch weder Kameras noch Computer können Bilder sehen. Sie verfügen nur über Zahlenwerte, die sie nach vorgegebenen Verfahren miteinander verrechnen. Wenn dabei die gewünschten Bilder herauskommen, so liegt es daran, dass die Entwickler von Kameras und Software verstehen, was sie tun: Sie finden geeignete Algorithmen und mathematische Formeln, die das richtige Ergebnis liefern. (Wobei das heutzutage, da immer mehr Funktionen von neuronalen Netzen übernommen werden, nur noch eingeschränkt gilt. Neuronale Netze werden nicht programmiert, sondern entstehen in Verfahren des maschinellen Lernens, so dass die Entwickler eher Schuldirektoren gleichen, die fähige Lehrer einstellen und Lehrpläne schreiben, aber dann nur noch darauf achten, dass niemand dummes Zeug macht, bis sie den Absolventen ihre Abschlusszeugnisse überreichen.)
Ähnliches gilt für Testverfahren. Als ich vor vielen Jahren Methoden entwickelte, die Bildqualität von Digitalkameras messtechnisch zu erfassen, suchte ich beispielsweise nach einer geeigneten Formel, das Farbrauschen unabhängig vom Luminanzrauschen zu erfassen, was sonst niemand machte und das bis heute nicht oft getan wird. Ich musste eine Zeitlang darüber nachgrübeln und verschiedene Ideen ausprobieren, bis ich einen Algorithmus gefunden hatte, mit dem meine Auswertungssoftware die richtigen Werte lieferte – „richtig“ in dem Sinne, dass einer Kamera, deren Fotos ein visuell stärkeres Farbrauschen als die Fotos eines anderen Modells zeigten, auch ein höherer Messwert zugeordnet wurde. Entscheidend ist immer die visuelle Wahrnehmung, und wenn Rechenergebnis und Wahrnehmung nicht zusammenpassen, dann stimmt die Formel nicht.
Jüngst stieß ich nun auf ein weiteres Problem dieser Art, nämlich darum, den Unterschied zweier Farben zahlenmäßig zu beschreiben. Und zwar nicht allein der reinen Farben des Spektrums, denen jeweils eine einzige Wellenlänge entspricht – was zwar keineswegs trivial, aber doch einfacher wäre –, sondern auch weniger gesättigte Farben bis zu den unbunten Grautönen sowie Schwarz und Weiß. Also kurz gesagt allen im RGB-Farbmodell darstellbaren Farben. (Genau genommen will ich die Farbanmutung von Fotos charakterisieren und Bilder mit ähnlichen Farben identifizieren; der Vergleich einzelner Farben ist nur ein – allerdings wichtiger – Teil davon.)
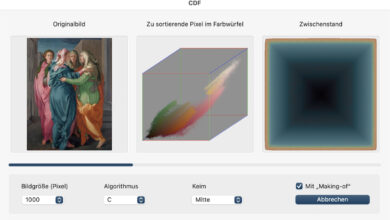
Jedenfalls: Wie geht man da vor? Wer mathematisch denkt, dem fällt sofort eine Lösung ein. Das RGB-Modell ist ein Raum mit drei Dimensionen, den Helligkeiten der Grundfarben Rot, Grün und Blau. Jede RGB-Farbe ist ein Punkt in diesem Raum und der Abstand zweier Punkte lässt sich leicht nach dem Satz des Pythagoras ausrechnen. Aber diese Formel liefert nicht immer das erwartete Ergebnis.

In diesem Beispiel beträgt die Entfernung des helleren Grau vom dunkleren Grau 60,6, während das blasse Grün rechts in einer Entfernung von nur 50,0 liegt und damit als ähnlicher anzusehen wäre. Aber das entspricht kaum unserer Intuition – oder jedenfalls nicht meiner, denn mir erscheinen die beiden Grauwerte ähnlicher, während das Grün eine ganz andere Farbe ist.
Es läge nahe, die Farben zum Zwecke des Vergleichs in ein anderes Farbmodell umzurechnen, zum Beispiel HSL (für Hue, Saturation und Luminance, also Farbton – angegeben als Farbwinkel im Farbkreis –, Sättigung und Helligkeit). Dann könnte man diese Parameter miteinander vergleichen und Unterschiede des Farbtons, auf die wir besonders empfindlich reagieren, entsprechend stärker gewichten als Unterschiede von Sättigung oder Helligkeit. Eine Besonderheit bieten hier die wenig gesättigten Farben: Selbst wenn die Sättigung gleich Null ist, muss ein Wert für den Farbwinkel (Hue) zugeordnet werden, obwohl er dann keine Rolle spielt und jeder beliebige Wert dieselbe Farbe ergäbe; per Definition wird er dann auf 0 Grad gesetzt, was der Farbe Rot entspricht. Schwierigkeiten gibt es bei Farben, deren Sättigung nur fast Null ist, beispielsweise den RGB-Farben [101,100,100], [100,101,100] und [100,100,101]. Schon kleinste Unterschiede lassen dann den Farbwinkel heftig rotieren:

Visuell sind diese drei Farben, in denen jeweils eine Grundfarbe minimal dominiert, kaum zu unterscheiden, aber wenn man sie in das HSL-Farbmodell umrechnet und nach dem Farbwinkel geht, handelt es sich um Varianten von Rot (0 Grad), Grün (120 Grad) und Blau (240 Grad). Gewichtet man den Farbwinkel dann auch noch stärker als die Sättigung und die Helligkeit, kommt man unweigerlich zum Ergebnis, dass es sich um ganz unterschiedliche Farben handelt.
Der althergebrachte Standard für Farbunterschiede ist Delta E, das aus dem Abstand im L*a*b*-Farbmodell berechnet wird, aber dass auch dieser Wert nicht immer unserem visuellen Empfinden entspricht, ist schon lange bekannt. Es gibt Alternativen, nur sind sie recht komplex. Ich werde erst einmal mit einer Formel arbeiten, die Unterschiede im Farbton zwar höher als solche der Sättigung oder Luminanz gewichtet, aber um so schwächer, je niedriger das Minimum der Sättigungswerte beider Farben ist. Schauen wir mal, wie weit ich damit komme …







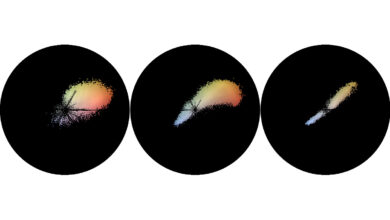


Rin interessanter Einblick in Ihre Arbeit, vielen Dank. Haben die Probleme zwischen der algorithmischen Farb-Modellierung und der Wahrnehmung vielleicht damit zu tunn, dass leztztere nicht linear arbeitet?
Das spielt eine Rolle, ja. Weniger bei den Tonwerten, denn in RGB-Bildern sind die linearen Rohdaten aus der Kamera bereits in eine an unser Empfinden angepasste annähernd logarithmische Skala umgewandelt. Bei den Farben spielt es aber eine Rolle. Schon wenn ich mich beim Farbvergleich auf Spektralfarben, also reine Farbtöne beschränken würde, könnte ich nicht einfach Differenzen zwischen Wellenlängen berechnen, denn wir differenzieren nicht alle Farben gleich fein. Einerseits aus physiologischen Gründen, also aufgrund der Art und Weise, wie die Zellen in unserer Netzhaut Farben unterscheiden, aber auch aus kulturellen Gründen.
Inwieweit die Farbwörter einer Sprache die Wahrnehmung ihrer Sprecher beeinflussen, ist zwar umstritten – wenn man im direkten Vergleich Farben unterscheiden soll, scheint es keine große Rolle zu spielen, über welche Wörter man dafür verfügt. Wenn man sich aber an eine Farbe erinnern soll, ist es durchaus hilfreich, wenn man sie auch benennen kann und nicht allein auf das visuelle Gedächtnis angewiesen ist. Das ist auch individuell unterschiedlich: Es klingt zwar klischeehaft, ist aber trotzdem nicht falsch, dass Frauen, denen hundert Schattierungen von Lippenstiftfarben vertraut sind, hier feinere Unterscheidungen treffen können als die meisten Männer (oder Frauen mit weniger ausgeprägtem Interesse an Lippenstiftfarben, was das betrifft).