Bildkritik: Die Wiederkehr des Fluchs der eingerollten Ecke
In seinem letzten Beitrag hatte Doc Baumann hier ein Beispiel aus der Werbung vorgestellt, das – wie so viele andere – einen fehlerhaft dargestellten Eckenknick verwendete. Und er zeigte gleich auch noch, wie man es einfacher und besser machten könnte. Aber leider war seine Lösung ebenfalls nicht ganz richtig; sie sah zwar schön aus, war aber dennoch falsch konstruiert. Daher überlässt Doc Baumann diesmal Ludwig Wiese das Wort für einen Gastbeitrag, in dem der demonstriert, wie eine solche Ecke wirklich aussehen sollte.

Bereits in seinem Kommentar auf der DOCMA-Webseite hatte Ludwig Wiese darauf hingewiesen, dass meine Ecke zwar perfekt aussehe – es aber leider nicht sei. Seine Erklärung dazu war völlig korrekt, aber ohne entsprechende Abbildungen doch etwas schwer nachzuvollziehen. Daher bat ich ihn, die richtige Konstruktion noch einmal ausführlich hier vorzustellen, und freundlicherweise sagte er auch gleich zu.
Zu entschuldigen gibt es bei meinem Fehler nichts. Ich hatte mich so sehr auf das Problem der zu langen Knick-Seiten konzentriert, dass ich bei meiner vermeintlichen Lösung ausschließlich auf diesen Aspekt geachtet habe. Schauen wir uns also an, wie man richtig vorgeht.
Der Fotobeweis
Ehe ich die Vorgehensweise von Ludwig Wiese zeige, möchte ich Ihnen noch kurz den fotografischen Beleg dafür liefern, dass er recht hat.
Dazu habe ich eine solche Ecke in unterschiedlichen Positionen fotografiert (natürlich unter Zuhilfenahme eines Stativs), die Fotos als Ebenen in eine Datei eingefügt, zu einem Smartobjekt gemacht und so in einen Stapel geladen, und dann in Photoshops Ebenen-Menü (Smartobjekte > Stapelmodus) die passende Variante gewählt: Arithmetisches Mittel. Dabei ist es egal, wie und wo die Ecke geknickt wird, wie lang also die beiden Kanten sind, die an den rechten Winkel anschließen.

Wie Sie sehen, liegen alle Ecken auf einer geraden Linie, die die Ecke in ihrem ungefalteten Urspungszustand mit der verbindet, wenn sie vollständig umgeklappt ist und das Papier des Bogens berührt.

Erfahren Sie nun von Ludwig Wiese, warum das so ist und wie es geometrisch begründet wird.
Der geometrische Beweis
Das Bild von Doc Baumann mit dem einfachen Eckenknick wirkt mit Schattenwurf und Abdunklung perfekt, ist jedoch in dieser Form in der Realität nicht möglich. Schön, aber falsch.
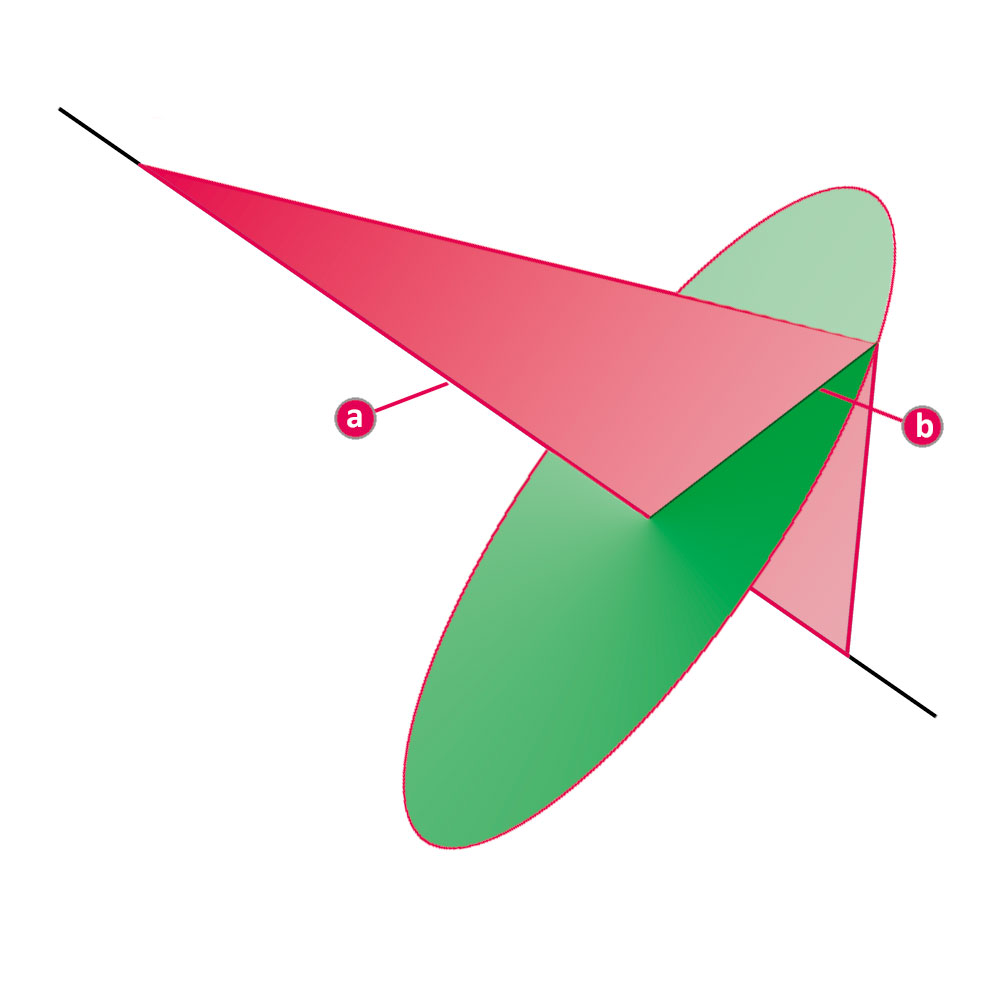
1. Der Beweis lässt sich mit den Regeln der Geometrie führen: Wenn ein rechtwinkliges Dreieck um die Hypotenuse (a) – also die dem rechten Winkel gegenüberliegende Seite – rotiert, wird die Höhe (b) über der Hypotenuse zum Radius einer Kreisfläche im Raum.
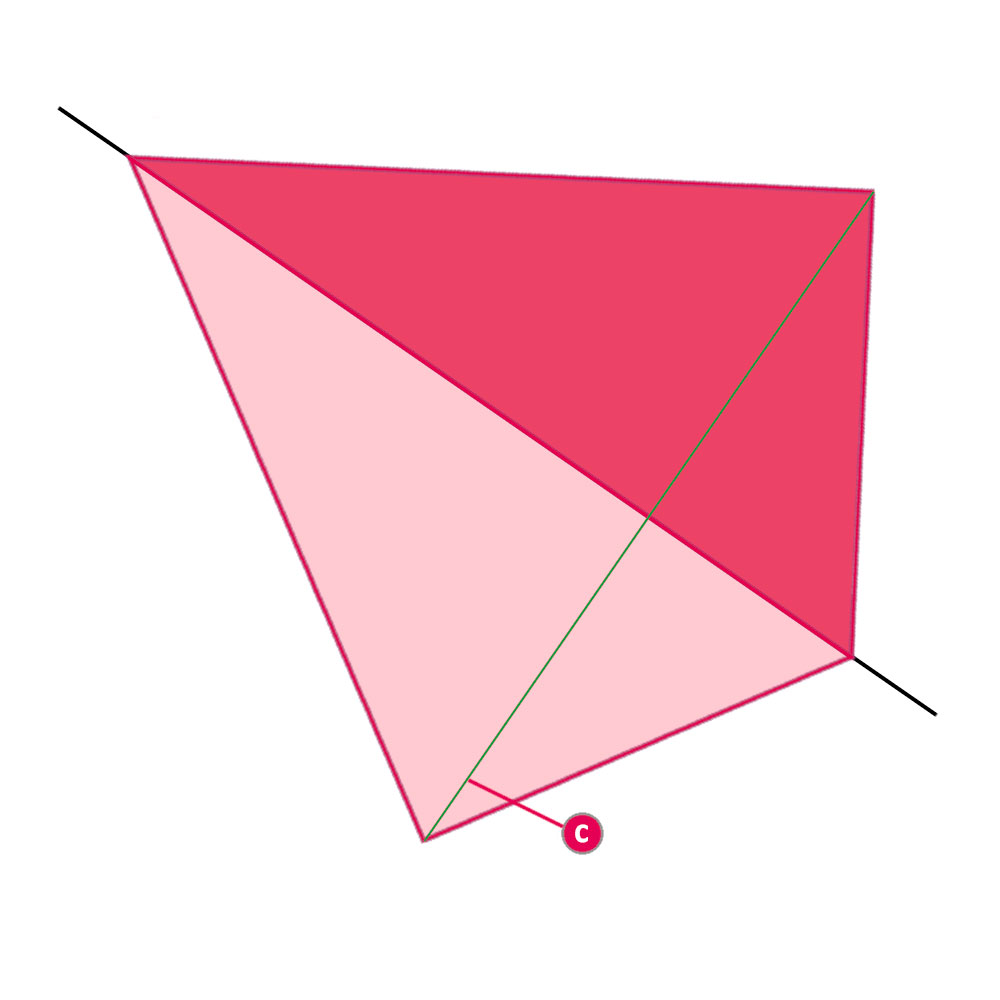
2. Schaut man im rechten Winkel auf die Hypotenuse, erscheint die Kreisfläche als Gerade (c) mit der Länge des Durchmessers.

3. Nun die Anwendung: Die abgeknickte Ecke hat die Form eines rechtwinkligen Dreiecks, bei dem die Knickkante die Hypotenuse ist.

4. Den Knickvorgang kann man sich als Rotation um die Hypotenuse vorstellen. Damit beschreibt die Papierecke in der Draufsicht eine Gerade von der nicht geknickten bis zur voll umgeknickten Position. Beim einfachen Eckenknick muss die Ecke immer auf dieser Geraden liegen.

5. Im von Doc Baumann konstruierten Bild liegt die Ecke aber darüber. Somit kann diese Darstellung nicht der Realität entsprechen.

6. Wenn man die untere Seite des Knicks bis zur Geraden verkürzt, erreicht man eine korrekte Darstellung.

7. Aber wozu dieser ganze Aufwand für die korrekte Darstellung? Der Unterschied zwischen dem falschen und richtigen Knick scheint kaum aufzufallen. Doch wie so häufig bei Bildbearbeitungen und -montagen, hatte ich bei der Betrachtung der ursprünglichen Darstellung das unbestimmte Gefühl, dass irgendetwas nicht stimmt.






Die Hypothenuse ist richtig beschrieben (die Seite gegenüber dem rechten Winkel), doch in der Grafik wird sie mit (a) gekennzeichnet. Das ist falsch. Richtig wäre üblicherweise (c), denn (a) ist eine Kathete. Also wäre ein (c) bei der längsten Seite, eben der Hypothenuse, korrekt, (a) und (b) sind jedoch Katheten.
Ich fürchte, Sie haben die Grafik von Ludwig Wiese falsch interpretiert: Der rechte Winkel (des Papierbogens) ist der rechts oben (links oberhalb des (b) – nicht derjenige, der in der Bildmitte im Zentrum des als Ellipse dargestellten Kreises liegt. Die Hypothenuse ist mit (a) richtig bezeichnet und verläuft von links oben nach rechts unten, wo sie zum Teil von dem grünen Rotationskreis verdeckt wird; auch diese Linie rechts unten gehört noch zu (a). (b) ist keine Kathete, sondern die Höhe, die auf der Hypothenuse aufsetzt und zum rechten Winkel verläuft. In meiner Aufmacherillustration wird das vielleicht noch mal deutlicher, wo ich die Grafik so gedreht habe, dass die Hypothenuse (a) parallel zur Knickkante der Ecke des Papierbogens verläuft.
a² + b² = c²
Warum die Standardbezeichnung der 3 Seiten eines rechtwinkligen Dreiecks neu erfinden?
Die Namen der Strecken sind Schall und Rauch; man kann sie auch Peter, Paul und Marie nennen, ohne dass sich irgendetwas ändert. a, b und c (wobei c die Hypothenuse des rechtwinkligen Dreiecks ist) sind die üblichen Bezeichnungen im Satz des Pythagoras, der hier allerdings keine Rolle spielt. In der Trigonometrie wären es a, g und h (mit h als Hypothenuse), aber auch die Trigonometrie spielt hier keine Rolle. Im allgemeinen Fall benennt man die Strecken des Dreiecks meist mit a, b und c (entgegen dem Uhrzeigersinn), wobei es einem freigestellt ist, bei welcher Strecke man anfängt. Man könnte dafür argumentieren, die hier b genannte Höhe über a mit h zu bezeichnen, da dieser Buchstabe oft für eine Höhe im Dreieck verwendet wird, aber wie gesagt: Die Namen sind völlig beliebig und die hier getroffenen Feststellungen sind korrekt, egal wie man die einzelnen Strecken bezeichnet. Da hier überhaupt nur zwei Strecken relevant sind, kann man sie also auch einfach a und b nennen. So handhaben wir das in DOCMA ja generell: Wenn es zwei Details in einer Illustration gibt, die wir einzeln bezeichnen wollen, nennen wir sie a und b.
Die Erklärung von Ludwig Wiese ist völlig korrekt, für die Darstellung und damit für die Größe der Katheten ist aber auf alle Fälle noch der Blickwinkel entscheident.
Hi hi, Eselsohren bleiben Eselshohren auch wenn sie digital sind 🙂
LG Bernhard
https://deramateurphotograph.de/
Die umgeklappte Ecke bewegt sich nur bei senkrechter Draufsicht auf einer Geraden. Senkt man die Ansicht soweit, bis die optische Achse des Auges auf der Knickfalte liegt, dann bewegt sich die umgeklappte Ecke auf einem Kreisbogen mit dem Mittelpunkt auf der Achse. In allen Blickwinkeln dazwischen geht die Gerade als Ellipse sukzessive in den Kreisbogen über. Geht man mit dem Blickwinkel aus der imaginären senkrechten Ebene durch die Falte nach rechts und blickt dabei entsprechend etwas nach links, dann erfährt die Ellipse eine Verkippung nach vorne in Richtung Blattmitte. Geht man mit dem Auge noch stärker nach rechts mit Blickrichtung noch weiter nach links, bis die Knickfalte exakt rechtwinklig zur Blickrichtung liegt, geht auch diese gekippte Ellipse ebenfalls in eine Gerade über.
Fazit: Doc Baumanns Ecke lag mit Sicherheit auf einer dieser möglichen Ellipsen und seine Abbildung war folglich korrekt. Die grosse Frage ist die nach der entsprechenden Blickrichtung zu dieser Ellipse.