Bildbearbeitung und die Tücken der Mathematik

In der neuen DOCMA 83 zeigt Doc Baumann in seiner Photoshop-Sprechstunde, wie sich geplante Windräder an der richtigen Stelle und in der später sichtbaren Höhe in ein Landschaftsfoto einmontieren lassen. Beim Austüfteln der Lösung stolperte er allerdings zunächst über die Tücken der Mathematik.

Wenn ich für meine Photoshop-Sprechstunde Anfragen unserer Leserinnen und Leser erhalte, reichen meistens meine Kenntnis der Software und dreieinhalb Jahrzehnte Erfahrung mit digitaler Bildbearbeitung aus, um die richtige Lösung vorschlagen zu können. Manchmal ist es aber auch anders. So hatte ich in meinem Blog-Beitrag Mitte April 2018 auf ein weiteres Tutorial aus DOCMA 83 hingewiesen, bei dem ich weniger die Tücken der Mathematik als die der Geometrie zu bewältigen hatte. In beiden Fällen geht es um eine korrekte perspektivische Konstruktion.

Im Fall der Windräder hatte eine Leserin – und gute Freundin von mir – nachgefragt, wie ihre Bürgerinitiative gegen Windräder der Bevölkerung visuell verdeutlichen könnte, wie diese Anlagen nach ihrer geplanten Errichtung aussehen würden. Die Montagen sollten nicht übertreiben, sondern den späteren Zustand glaubwürdig dokumentieren.

Vorsichtshalber hatte sie ihre Frage mit dem Anhang ergänzt: „ … wohl wissend, wie Du in dieser Angelegenheit denkst“. In der Tat würde ich solche Initiativen eigentlich nicht unterstützen. Auch mich stört gelegentlich der Anblick von gigantischen Windrädern auf ansonsten – zumindest scheinbar – naturbelassenen Waldhügeln, und die „Verspargerlung der Landschaft“ ist gewiss keine Freude fürs Auge. Aber solange es keine realistischen Alternativen gibt, denke ich, dass wir Windräder akzeptieren müssen – ich habe zu Hause selbst etliche im Blickfeld. Denn weiterer CO2-Ausstoß führt ebenso in die Katastrophe wie die Nutzung der Kernkraft. Vielleicht gibt’s ja irgendwann doch mal die kalte Fusion oder einen Anihilations-Generator – der würde dann auch gleich das Abfallproblem lösen.

Die Tücken der Mathematik: Dreisatz

Da ich vor vielen Jahren schon einmal ein ähnliches Tutorial verfasst hatte, erwartete ich keine großen Probleme bei der Lösung. Allerdings musste ich feststellen, dass die Rahmenbedingungen nun ganz andere waren: Damals hatte ich die Landschaft von einem Hügel aus aufgenommen und konnte auf dem Foto alle Standorte der geplanten Anlagen deutlich erkennen. Doch im aktuellen Fall war das ganz anders, weil die Windräder hinter einer Hügelkette errichtet werden sollen, die Standorte also nicht zu sehen waren. Nun gut, dieses Problem konnte ich schließlich mit geometrischen Mitteln lösen.

Komplizierter war es dagegen mit der Ermittlung der scheinbaren Höhe. Dank Google Earth – ohne das Programm geht gar nichts – konnte ich einiges fixieren: Den Standort des Fotografen, die Standorte der Windräder, Gebäude, die auch auf dem Landschaftsfoto zu identifizieren waren. Mit Hilfe der Mess-Pfade in Google Earth ließen sich zusätzlich feststellen: Die Entfernung jeder Windradanlage vom Kamerastandort, und ebenso die Entfernung bestimmter Gebäude (und ihrer Längen) von diesem Punkt aus.

Zudem wusste ich, dass die Nabenhöhe der Windräder 145 Meter sein würde. Damit hatte ich eigentlich genügend Daten. Nun brauchte ich nur noch schlichte Dreisatz-Rechnung (dachte ich): Die Firstlänge eines exakt im rechten Winkel zur Blickachse stehenden Gebäudes konnte ich auf Google Earth mit 77,1 Metern ausmessen – in Foto bestimmte ich sie mit Photoshops Messwerkzeug auf 72 Millimeter. Ich hätte auch das Pixelmaß zugrundlegen können, das läuft am Ende aufs Gleiche raus. Zudem wusste ich dank Google-Earth-Messung, dass das Gebäude 575 Meter von der Kamera entfernt war. Auf die gleiche Weise konnte ich ermitteln, wie weit es zu Windrad A ist: 2.520 Meter.

Erster Schritt: Die Nabelhöhe (145) entspricht 188% der Firstlänge (77,1) – 145/77,1=188. Stände das Windrad in der Entfernung des Hauses, wäre es im Bild also 72 Millimeter × 1,88 groß, das ergibt 134 mm. Das war ja einfach.

Zweiter Schritt: Wenn das Windrad bei 575 Metern Entfernung im Bild eine Höhe von 134 mm hat, muss es bei einer Entfernung von 2.520 Metern die Höhe x haben. Abermals ein schlichter Dreisatz:

134 : 575 = x : 2.520. Ergebnis: 58 mm. Auch das war ja auch einfach … oder?

Nehmen wir ein weiteres Windrad, das mit über dreieinhalb Kilometern deutlich weiter entfernt ist. Die Formel ändert sich dann nur geringfügig:

134 : 575 = x : 3.688. Das Ergebnis: 86 mm. Was nun allerdings seltsam ist. Ich hatte die entsprechende Formel in Excel eingegeben, und nun stellte ich fest: Je weiter das Windrad vom Kamerastandort entfernt ist, um so größer erscheint es im Bild! Dabei sollte es doch kleiner werden. Die Tücken der Mathematik. Da konnte etwas nicht stimmen. Ich grübelte und experimentierte, aber es kamen immer dieselben – und offensichtlich falschen – Werte heraus.

Die Tücken der Mathematik: With a little help from my friend

Schließlich war ich hinreichend verzweifelt, um einem Freund mit Informatikstudium eine Mail mit dem Problem zu schicken und um Hilfestellung zu bitten.

Derweil dachte ich selbst weiter nach. Warum auch immer, mein Dreisatz musste falsch sein. Also probierte ich es schließlich einmal andersherum:

Höhe des in Hausentfernung konstruierten Windrades im Foto (134 mm) multipliziert mit der Aufnahmeentfernung zum Haus (575 m), das Ergebnis dividiert durch die Entfernung zum geplanten Windrad (2.520 m). Also:

(134×575)/2.520. Das Ergebnis: 30 Millimeter. Na ja, kann stimmen oder auch nicht. Vielversprechend war schon einmal, dass mit dieser Formel die Windräder in der Montage mit zunehmender Entfernung kleiner wurden, das bei 3,6 km Entfernung sollte nun 21 mm hoch sein. Aber stimmte diese Formel tatsächlich? (Den umgekehrten Dreisatz können Sie im Web direkt berechnen lassen, etwa auf dieser Seite.)

Kurz darauf traf die ausführliche Antwort meines Freundes mit einer langen Ableitung ein. Zu meiner großen Erleichterung war er auf trigonometrischem Weg durch Berechnung der Sichtwinkel zum selben Ergebnis gelangt wie ich, und da seine Formel bis auf acht Stellen hinter dem Komma dieselben Werte ergab wie meine, muss es so wohl stimmen. Erst jetzt war ich sicher, meine neu gefundene Formel für die Montage verwenden zu können. (Seine Ableitung finden Sie weiter unten.) Ich wollte natürlich seine Hilfestellung angemessen zitieren, aber er meinte abwehrend: „Nun ja, das Technische der Herleitung haben wir wohl in der Obersekunda gelernt. Also bitte nicht meinen Namen erwähnen.“

Die Tücken der Mathematik: Gefühl und Verstand

Warum nun dieser umgekehrte Dreisatz der richtige Weg ist, habe ich allerdings immer noch nicht kapiert. Nach meinem Bauchgefühl war der erste Dreisatz richtig – aber auf Gefühle kann man sich in der Mathematik offenbar nicht immer verlassen.

Wenn Sie das nicht glauben, hier ein einfaches Beispiel. Ich kenne die richtige Lösung seit vielen Jahren, aber sie läuft meiner Vorstellungskraft noch immer völlig zuwider. Stellen Sie sich vor, Sie legen einen Fußball mit 20 Zentimetern Durchmesser auf den Tisch. Dann nehmen Sie einen Faden und winden ihn einmal um den Äquator des Balls. Sie können auch ein Maßband verwenden, dann lässt sich das Ergebnis direkt ablesen – der Umfang des Ball beträgt 63 Zentimeter. Nun verlängern Sie den Faden so, dass er überall 15 Zentimeter vom Ball entfernt ist, so dass Sie mit ihrer Hand bequem zwischen Ball und Faden greifen können. Die Länge des Fadens beträgt nun 157 Zentimeter, er ist also 94 Zentimeter länger als zuvor.

Nun versuchen Sie sich vorzustellen, Sie würden einen sehr viel längeren Faden einmal um den Erdäquator wickeln. Mit der Hilfe von Freunden (dabei brauchen Sie allerdings eine ganze Menge von ihnen) sorgen Sie dann dafür, dass auch dieser Faden überall einen Abstand von 15 Zentimetern zur Erdoberfläche bekommt (der Einfachheit halber gehen wir davon aus, die Erde sei eine glatte Kugel). Und nun die Preisfrage: Um welche Strecke müssen Sie diesen Faden verlängern, damit er ebenfalls überall diese 15 Zentimeter Abstand zur Erdoberfläche hat? Bedenken Sie dabei: Der Umfang der Erde beträgt das 63-Millionen-fache des Fußballs. Die Antwort auf diese Frage und eine kleine Tabelle finden Sie ganz am Ende dieses Textes. Aber vorher erst mal schätzen, ehe Sie die Lösung nachschlagen!

Trigonometrische Ableitung

Die Spitze der Windkraftanlagen W1 und W2 wird von der Kamera (rechts) unten den Blickwinkeln α1 und α2 gesehen.

α2 ist kleiner als α1, weil W2 weiter entfernt ist als W1.

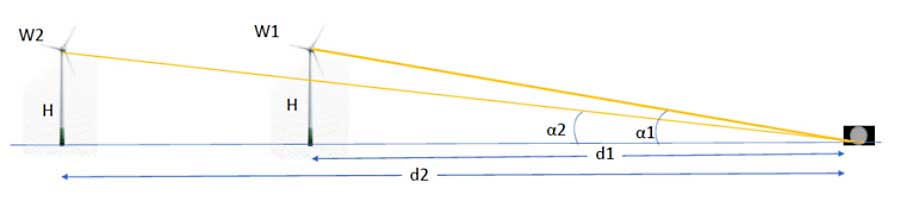
Berechnung:

tan α = H/d → α = arc tan H/d

Im Bild: x entspricht H/d. der Winkel π/2 entspricht 90°. Je größer H/d wird (je näher die Windmühle kommt), desto mehr nähert sich der Blickwinkel der Spitze 90°. Je größer der Abstand wird (H/d wird kleiner), desto mehr nähert sich der Blickwinkel 0°.

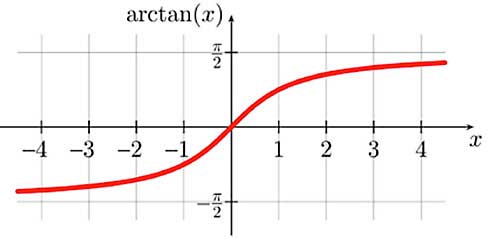
Bei kleinem H/d (also entweder kleiner Mühle oder großem Abstand, also kleinem Blickwinkel) ist die art tan-Kurve annähernd linear, also α = a ∙ H/d (a ist irgendein konstanter Faktor).

Was hat das mit dem Bild zu tun?

W1 und W1 werden auf eine gedachte Bildfläche projiziert. Objektiv ist das die Sensorfläche in der Kamera.

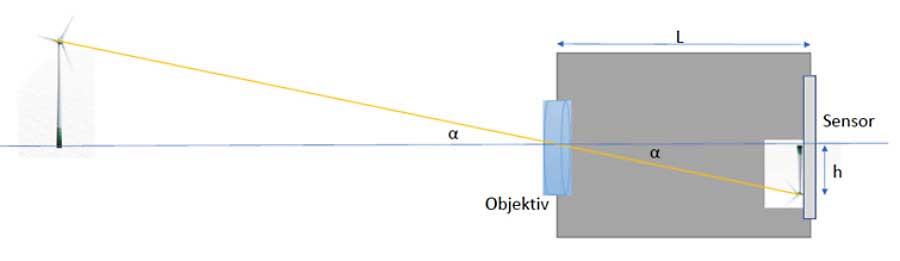
Wie groß erscheint die Windkraftanlage auf dem Sensor? Das hängt von der Geometrie der Kamera und der Optik der Linse ab. Auf jeden Fall gilt h ist proportional zu tan α. In der Lochkameraoptik des Bildes:

h = L ∙ tan α, wobei L die Länge der Kamera ist. Diese Frage ist von Bedeutung, wenn man wissen will, wo die Spitze der Mühle landet, wenn man die Kamera um einen Winkel kippt.

Gegeben sind

H, die Höhe der Windkraftanlage,

M, das Maß des Vergleichshauses

m, die Größe des Hauses auf dem Foto

d_W, die Distanz der WK-Anlage

d_Haus, die Distanz des Hauses

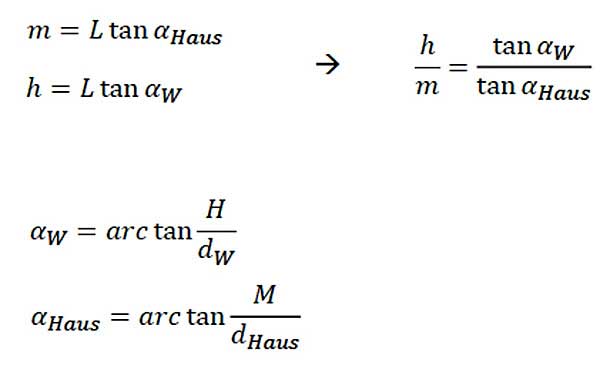
Gesucht: Wie viel mal größer als das Haus ist die Windkraftanlage auf dem Foto? Sei h die Größe der WK-Anlage auf dem Foto. Wir interessieren uns nicht für die Größe der Abbildung von Haus oder Mühle, sondern nur für das Verhältnis. Dann fliegen die trigonometrischen Funktionen wieder raus!

Lösung der Umfang-Frage

Ob Sie’s glauben oder nicht: Genau wie beim Fußball wird der um die Erde gewickelte Faden lediglich um 94 Zentimeter länger, wenn er überall 15 Zentimeter Abstand zur Erdkugel bekommt.